Sundial Calculations

The precise construction of the Woodland Polar Dial is made possible by comprehension of the mechanics of the annual earth orbit around the sun, trigonometry, and an accurate clock.

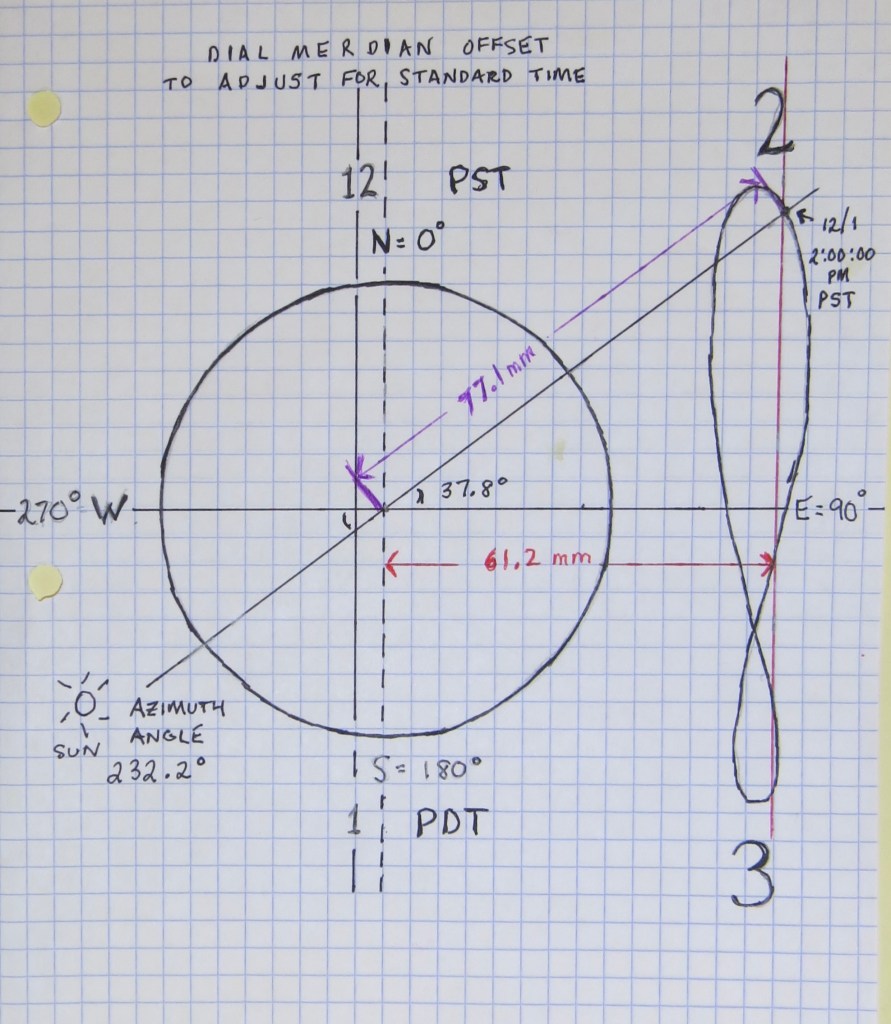
The picture above shows the shadow cast at 1:59:50 PM PST, 12/1/2023. How can the exact position of the shadow tip be calculated, so the dial could be constructed ?

The position of the shadow of the gnomon’s tip is dependent on the time of day, the declination of the sun (a measure of the axial tilt of the earth relative to the celestial equator), the sun’s elevation angle relative to the horizon, and the angle of the sun in the sky relative to the meridian (the azimuth angle). The meridian occurs at solar noon, when the sun is highest in the sky, and the sun always casts a a shadow due north-south. The length of the shadow is dependent on the elevation angle of the sun and the height of the gnomon. With an accurate clock, necessary to define longitude, the exact point of the gnomon shadow can be calculated for any time or date, allowing all the points of the sun’s course over the year to be determined. Sites such as the North American Sundial Society, ShadowsPro, and Sundial Primer offer fuller explanations.

δ = declination.            γ = hour angle.        φ =  latitude.   α = elevation angle

The hour angle is a measure of time.  T = local time, at the local Meridian.*  γ = 15° x (T – 12).  At 12 Noon, γ = 0.  At 2 PM, γ = + 30°.  At 9 AM, γ = -45°.

The azimuth angle is calculated from the hour angle, elevation angle, and declination.

α =  elevation angle = sin¯¹[ sinδ sinφ  + cosδ cosφ cosγ]

β = azimuth angle =  cos¯¹ [(sinδ cosφ – cosδ sinφ cosγ) / cosα ].  If γ is negative, β is the answer; if γ is positive, then final answer is 360° – β.

As mentioned in the Topic Equinoxes, a polar dial with a rod gnomon anywhere in the world is equivalent to a horizontal plane with a vertical pole on the Equator. This makes calculation of the azimuth angle simpler, because the contribution of latitude is eliminated.

Since on the Equator φ  = 0°;  sin 0°= 0, and cos 0° =1 .  Therefore:

  α = sin¯¹ [ 0 + cosδ cosγ]

 β = cos¯¹[ sinδ – 0 / cosα] =  cos¯¹ (sinδ/cosα).

Taking the simple example of a polar dial at sunrise on the equinox:  declination δ = 0; at 6 AM, γ= -90°; so, since sin 0° =0 and cos 0° =1 : 

α  = sin¯¹ [ (1)( cos (-90°)] =  0 Radians  

β = cos¯¹[ 0/1 Radians] = 1.5708 Radians = 90°.         

Calculators, by default, give arcsin and arccos in radians, not degrees.

The azimuth angle is the angle in degrees from which sunlight is coming from. By convention, due North is 0° (or 360°), due East is 90°, due South is 180°. At any northern hemisphere solar noon meridian, the azimuth angle is thus always 180°.

So, for the polar dial on the equinox at 6 AM, the azimuth angle is 90° ; the sunlight is coming from due East.

Similarly, since at 6 PM on the Equinox, γ= +90°, similar calculations also give β = 1.5708 Radians = 90°.  However, as noted above, when γ is positive, the azimuth angle = 360° – β = 270°.  Sunlight is coming from due West ; watch the videos of the polar dial on the Equinoxes to confirm this.

When doing sundial calculations and the answer does not make sense, it is often because you need to convert degrees to radians or vice versa, or need to subtract degrees from 360.

The azimuth angle can be computed for any day and any hour.  What is the azimuth angle at 2 PM, PST, on December 1st ?  

γ = +30°           δ on 12/1 (from declination table) = -20.9°    

α = sin¯¹ (cosδ cosγ) = sin¯¹[(.934)(.866)=   0.942 Radians

β=  cos¯¹[sinδ/cosα) =  cos¯¹(-.357/0.580) = 2.23 Radians = 127.8 °

Since γ is positive,  azimuth angle = 360 – 127.8 = 232.2°.

So, the shadow at 2 PM, 12/1, will lie along this line, at an angle 37.8° from the E-W horizontal equinox declination line:

If the length of the shadow is known, the tip of the shadow can be determined.  The dial gnomon height = 106 mm.  The elevation angle, α, has already been determined for our analogous horizontal dial at the equator, so the length L of the shadow is  tanα = 106/L.

L = 77.1 mm.

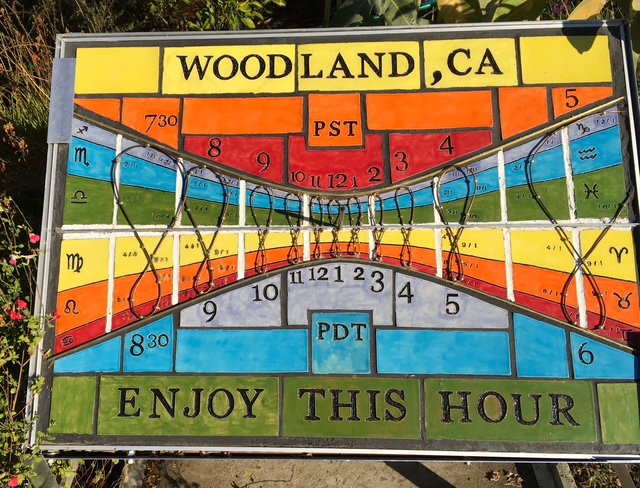
Another feature of a polar dial is that , regardless of the declination of the sun, the shadow of the gnomon in the east-west, horizontal dimension is the same throughout the year for any particular solar  time.  Many polar dials have a plate as a gnomon, perpendicular to the dial surface and parallel to the earth’s axis. Since the plate gnomon is parallel to the earth’s axis, the hour lines are always vertical, and it will cast a vertical shadow.  Knowing the formula d = (H) tan T°, where d = horizontal distance of cast shadow, H = gnomon height, and T° is the hour angle in degrees, hour lines can be plotted for Noon (T° = 0), 11 AM (T°= -15°), 1 PM (T°= +15 °) and so forth. The plate gnomon cast hour line shadows with a vertical N-S edge throughout the day. Remember this is based local meridian, so if standard time hour lines are desired, the gnomon must be moved east or west, depending on the longitude of the dial.  This is a fine polar dial in London :

Here is a mammoth polar dial in Melbourne, Australia. Since the plate gnomon is parallel to the earth’s axis, it has vertical hour lines. Since a polar dial casts very long shadows early and late, the dial edges are curved to capture the shadow, which otherwise would stretch into infinity near dawn and dusk:

By changing the plate gnomon to a rod gnomon centered on the equinox declination line, the east-west length of the shadow is the same for any specific hour angle throughout the year, but the diagonal length of the shadow will vary with the declination of the sun.

On a sundial, time is determined by west-east travel of the shadow. The north-south excursion is caused by axial tilt, and the shape of the analemmas, reflecting the Equation of Time, is a combination of axial tilt and the elliptical orbit of the earth. Consequently, from these effects, the time from one solar noon to the next can be up to 29 seconds longer or 22 seconds shorter than 24 hours, regardless of the meridian.

The horizontal distance of the shadow, d, is d=  (Height gnomon) (tan t°), where t° is the hour angle in degrees.  So, for 2:00 PM on December 1st, d = (106 mm) tan 30° =  61.2 mm .

This is a second way to determine the exact location of the shadow tip along the known azimuth angle shadow line, and confirms that the shadow length calculation was correct.

By using either the shadow length or the horizontal excursion length, the point of the shadow tip along the azimuth angle line can be defined:

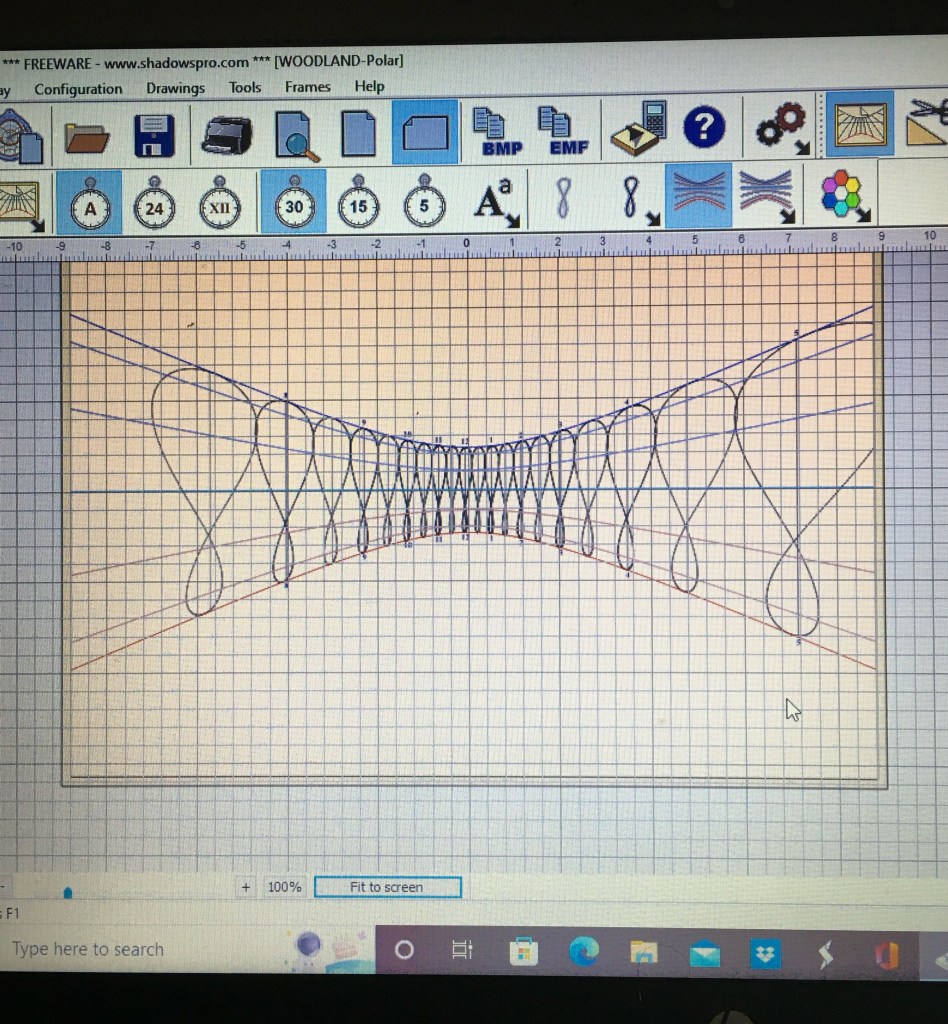
These calculations can be repeated for every day and time to plot each hour analemma and give a template for construction of the dial. ShadowsPro is free software that will calculate and plot all this data for any location. It is a treasure trove for making sundials of all types.

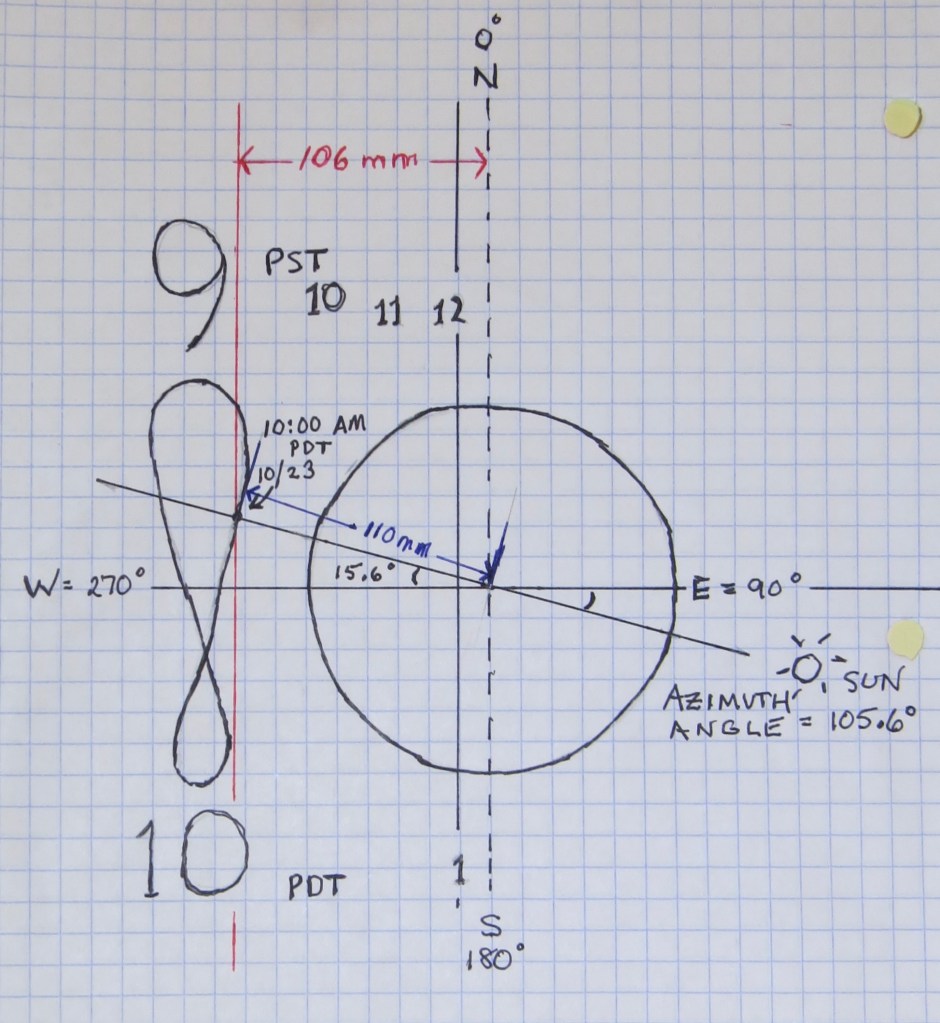
As another example, here it is 10:00 AM PDT, 10/23/2023, the day that the dial tracks the -11.2° declination line, separating the Zodiacal signs Libra (green) and Scorpio (blue):

Changing time to standard time = 9:00 AM:

γ= 15° x  -3 = -45°   δ = -11.2° gnomon hgt = 106 mm

α = sin¯¹ [(cos -11.2)(cos -45°) =   0.767  Radians

β = cos¯¹ (sin -11.2/cos .767) =  1.843 Radians = 105.6°      Since γ is negative, the azimuth angle is 105.6°, casting a shadow which is 15.6° above the EW horizontal declination line, pointing WNW.  The shadow length L,  = (tan .767 radians) =  106 mm/L = 110 mm.  

 Since horizontal distance d = (gnomon height)(tan γ) , and the tangent of -45° = -1, d= (106 mm)(-1) = -106 mm, so the d is west of the gnomon:

________________________ ___________________ ___________________ _______________

The precision of the dial has been verified by multiple measurements over the last two years, showing the shadow within 1-2 mm of the analemma line on the hour. The shadow can also be measured at any other day or time and compared to the expected calculated value. Here are shadow measurements taken on May 30, 2025, at 10:25:00 AM PDT :

Since the gnomon is .25 inch in diameter, 3 mm is added to the measurement to reach the shadow cast from dead center:

98.2 mm + 3 mm = 101.2 mm shadow length measured.

To calculate the expected shadow length :

Declination = δ on May 30 = +21°41’ = 21.68° Hour angle = γ  = 15° (9:25:00 AM PST -12) = 15°(9.417-12) =-38.745°  Elevation angle = α = sin¯¹[(cosδ)(cosγ)] = sin¯¹(.7248) = .8107 Radians = 46.45°

Shadow length L : tan(46.45°) = 106mm / L ;  Calculated shadow length = 100.8 mm

Using a template created by computer software, a sundial can be laser printed with great accuracy. To hand build a dial out of clay, metal, and wire is another thing. Of course, the ceramic tiles are just window dressing: the crux of the dial is precise placement of the declination lines and analemma wires, and then the exact orientation N-S, E-W, with a incline 36.66 degrees from the horizontal and a perpendicular gnomon. The winter declination line is placed 1-2 mm too far north; otherwise, all is good.

______________________________________________________________________________

The shadow can change rapidly, especially around the equinoxes and early and late in the day, so an accurate clock is essential. In just 15 seconds, from 7:00:00 AM to 7:00:15 AM on the Equinox, the shadow will shorten by 1.8 mm. A precise timepiece is a huge advantage for the modern sundialist. Cell phones and computer clocks are quite acurate. The U.S. Naval Observatory and the National Institute of Standards and Technology operate a website, time.gov, which gives the current Coordinated Universal Time (UTC). This time is based on the weighted average of over 300 world-wide atomic clocks, but is also adjusted by leap seconds to account for the difference between the International System of Units (SI) definition of a second (the energy released from the transition between the two hyperfine ground states of cesium 133) and the rotation of the earth, keeping UTC synchronized with the apparent position of the sun (astronomical time = UT1) . The site also shows how far off your device’s clock is from UTC. At the time of this writing, the iPad which I am using is -0.079 seconds different from UTC. This is quite acceptable for building a dial. **

______________________________________________________________________________

The inner courtyard of the National Institute of Standards and Technology in Gaithersburg, Maryland, is home to one of the most famous polar sundials in the world, the Briggs Commemorative Dial. Installed in 1948, it also converts solar time to standard time and was one of my inspirations to create the Woodland Dial.

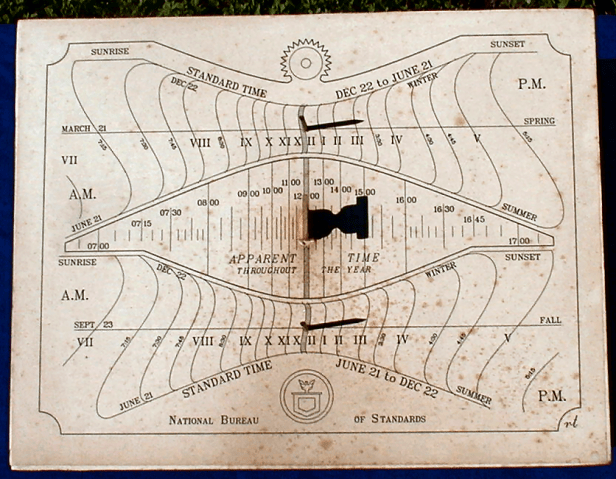
* The dial corrects the local meridian to standard time meridian , 120° W for the Pacific time zone.  The dial has been corrected for its 121° 47.4’ longitude by shifting its meridian to the east (1.8° x 4 min/degree =  7.2 minutes).

** Leap seconds are added to UTC to keep within +/- 0.9 seconds of UT1 (astronomical time), which varies due to irregularities in the earth-moon orbit, mostly due to slowing of the earth’s rotation over time, though melting polar ice caps may speed it up a little. International Atomic Time (TAI) does not add Leap Seconds. TAI is currently (as of May,2025) ahead of UTC by a whopping 37 seconds, making your cell phone a MUCH better timepiece for tracking the position of the sun and stars than a Cesium 133 Atomic Clock ! Moreover, if you used your basement atomic clock to calculate the above 5/30/25 shadow, time would be 10:25:37, the elevation angle would equal 46.58°, and the calculated shadow length would be 100.3 mm.  Since the actual sun position is determined by UTC ≈ UT1, the properly calculated shadow length = 100.8 mm .  The sundial measured dial shadow above was within 0.4 mm (101.2mm);  the cesium clock time calculated length was within 0.5 mm (100.3 mm).  So, at this time and date, the Woodland Polar Dial was a better timepiece than the atomic clock in calculating sun position.  Calculations were repeated on 6/5/25, at 3:14:00 PM PDT. Measured shadow length was 88.9 mm. Calculated shadow length using UTC time was 87.5 mm. Calculated length using atomic clock time of 3:14:37 was 88.1 mm, so at this afternoon time, the atomic clock was closer. Of all the challenges in constructing the dial, insuring that the gnomon is perfectly perpendicular, and stays that way, was one of the most daunting. It appears the gnomon is tilted slightly. Still, these numbers confirm the sundial’s accuracy to within approximately one minute from UTC.